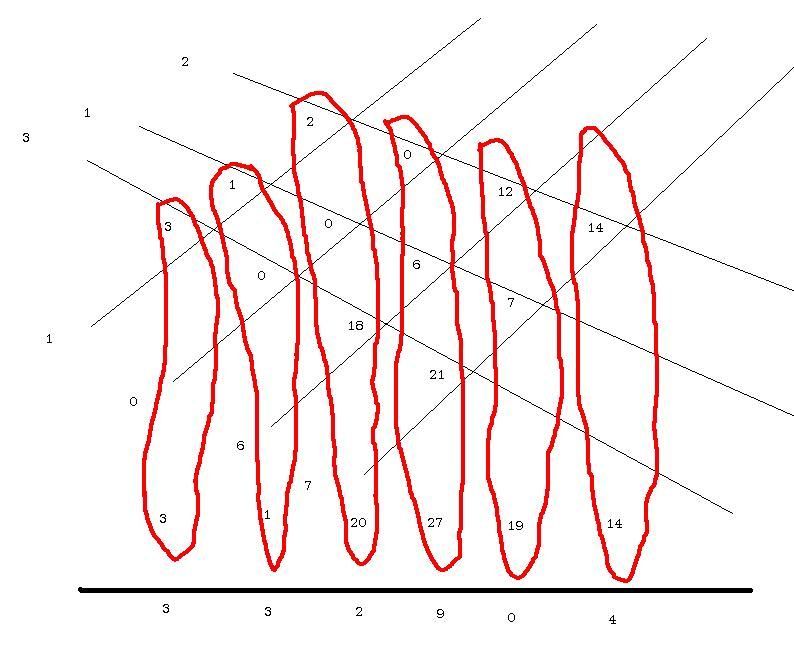
Visual Multiplication with Lines
10 inlägg
• Sida 1 av 1
Visual Multiplication with Lines
Kanske inte varken bättre eller sämre, men rätt kul sätt att multiplicera.
[youtube]http://www.youtube.com/watch?v=e-P5RGdjICo[/youtube]
[youtube]http://www.youtube.com/watch?v=e-P5RGdjICo[/youtube]
- Le_inimitable
- Inlägg: 1044
- Anslöt: 2008-10-26
imperativ skrev:För mig är den här uträkningen mer logisk och följsam än den jag lärt mig i skolan. Enklare att ta till sig också.
Min son och jag testade lite vi med och fann att metoden är helt klart logisk och användbar.
Det borde inte vara så värst komplicerar att visualisera i huvudet och därmed förbättra huvudräkningen...
Tycker de känns mer krångliga båda två men alla funkar ju olika.
Japanerna räknar förövrigt med tiotusen åt gången istället för vårat sätt med tusen. Därav använder de inte något ord för miljon utan lägger ihop deras ord för hundra och tiotusen istället: "hyaku" och "man" till hyakuman.
Går man högre upp har de dock ett eget ord för 100 miljoner nämligen "oku" så att vårat 1 miljard blir 10+oku (juuoku).
Japanerna räknar förövrigt med tiotusen åt gången istället för vårat sätt med tusen. Därav använder de inte något ord för miljon utan lägger ihop deras ord för hundra och tiotusen istället: "hyaku" och "man" till hyakuman.
Går man högre upp har de dock ett eget ord för 100 miljoner nämligen "oku" så att vårat 1 miljard blir 10+oku (juuoku).
+1imperativ skrev:För mig är den här uträkningen mer logisk och följsam än den jag lärt mig i skolan. Enklare att ta till sig också.
- Mellanvärld
- Inlägg: 1243
- Anslöt: 2010-11-28
- Ort: Göteborg
Om du börjar med multiplikation av två heltal, t ex 2 och 4, och ritar linjerna så ser du (förhoppningsvis) att det blir 8 korningar. Detta är jämförbart med när man ritar upp 2*4 kvadrater här i väst, vilket är vad vi brukar göra för att visualisera multiplikation.Moggy skrev:Nån som kan ge sig på en pedagogisk förklaring varför det funkar?
- Kod: Markera allt
Öst:
| | | |
-+-+-+-+- 1
| | | |
-+-+-+-+- 2
| | | |
1 2 3 4
Väst:
+-+-+-+-+
| | | | | 1
+-+-+-+-+
| | | | | 2
+-+-+-+-+
1 2 3 4
En grupp med korsningar är alltså en multiplikation. Men hur hänger det ihop med flersiffrig multiplikation? Uträkningen är egentligen inte så olik den vi gör när vi ställer upp en multiplikation som vi brukar göra. För att ta hans exempel, 21*13:
- Kod: Markera allt
21
*13
------
63
+21
------
273
Det är alltså precis samma algoritm, fast uttryckt på ett annat sätt.
Miche skrev:Arkimedes skrev:Här är en till
Den första begrep jag från början, men den Arkimedes visade förstår jag inte hur den kan funka...
Pedagogisk förklaring?
a * b = ?
a - (100 - b) = b - (100 - a)
Dessa är lika så det spelar ingen roll vilken vi använder så jag tar t ex
a - (100 - b) = a - 100 + b
Då har vi att
a * b = (a - 100 + b) * 100 + (100-a)*(100-b)
a * b = 100a -10000 + 100b + 10000 -100b -100a + a * b
Nu kan vi förkorta bort 100a mot -100 a, 10000 mot -10000, 100b mot -100b.
Kvar har vi a * b = a * b