imperativ skrev:Jag har faktiskt förlorat en argumentation om resultatet av 30 dividerat med ½ (som är lika med 60). Visst hade jag rätt, dock förlorade jag själva diskussionen. Ganska... pinsamt dåligt.

Det låter som mitt problem.
Jag argumenterar så dåligt att jag skulle förlora en diskussion om huruvida 1+1 är 2 eller 3 (om jag påstod att det vore 2 alltså).

Faktiskt så förlorade jag en diskussion om exakt det du skrev ovan, nyligen.
Personen menade att när man delar 30 i halvor så blir det 15. Jag tror det var engelsk text inblandad.
Jag fick inte till något argument och det verkade handla om språkfel på något sätt.

En annan person har sagt att 30 1/2 pint öl är detsamma som 15 pint, eftersom det står "trettio halva pint öl". Jag är för dålig på språk för att kunna argumentera, och det gör också att jag kan ha svårt att veta om jag har tolkat text/ord rätt.

******************

weasley:

Diskussion avknoppad härifrån: upprord-nar ... 12767.html

Bror Duktig skrev:Det låter som mitt problem.
Jag argumenterar så dåligt att jag skulle förlora en diskussion om huruvida 1+1 är 2 eller 3 (om jag påstod att det vore 2 alltså).

Ja, vadå då? Det beror helt på vilken algebra du väljer och vilken semantik du använder för siffersymbolerna.

Kvasir skrev:

Bror Duktig skrev:Det låter som mitt problem.
Jag argumenterar så dåligt att jag skulle förlora en diskussion om huruvida 1+1 är 2 eller 3 (om jag påstod att det vore 2 alltså).

Ja, vadå då? Det beror helt på vilken algebra du väljer och vilken semantik du använder för siffersymbolerna.

När blir 1+1=3?
I parrelationer kanske?
Jag vet inte vad semantik betyder.

Bror Duktig skrev:När blir 1+1=3?
I parrelationer kanske?
Jag vet inte vad semantik betyder.

Inom den "vanliga" matematiken så har man standardiserat vad både siffrorna och plustecknet betyder, men det är bara en konvention där. Inom mera generell matematik gör man inte alltid sådana förutsättningar. Man kan t.ex. definiera en algebra där plustecknet tolkas helt annorlunda än vanligt, så att t.ex. 1+1 = 3 och 2+2 = 1 och vad man nu kan tycka sig ha behov av. Likaså kan man tänka sig att siffrorna har annan betydelse än den vanliga, fast då börjar vi kanske gå in mera på logik än matematik.

Nu skrev jag förstås föregående inlägg bara för att retas med dig, eftersom detta är överkurs även för de flesta som lästa matematik på universitetsnivå.

Kvasir skrev:

Bror Duktig skrev:När blir 1+1=3?
I parrelationer kanske?
Jag vet inte vad semantik betyder.

Inom den "vanliga" matematiken så har man standardiserat vad både siffrorna och plustecknet betyder, men det är bara en konvention där. Inom mera generell matematik gör man inte alltid sådana förutsättningar. Man kan t.ex. definiera en algebra där plustecknet tolkas helt annorlunda än vanligt, så att t.ex. 1+1 = 3 och 2+2 = 1 och vad man nu kan tycka sig ha behov av. Likaså kan man tänka sig att siffrorna har annan betydelse än den vanliga, fast då börjar vi kanske gå in mera på logik än matematik.

Nu skrev jag förstås föregående inlägg bara för att retas med dig, eftersom detta är överkurs även för de flesta som lästa matematik på universitetsnivå.

Tror snarare att det är du som är ägd Kvasir om du anser att det är överkurs på universitetet. Jag minns att jag läste en bok på högstadiet där de förklarade sånt där på ett väldigt enkelt sätt så att även barn skulle kunna förstå det. Exempelvis stod det om ringar, ditt exempel 2+2=1 gäller i ringen Z3.

tveskägg skrev: Tror snarare att det är du som är ägd Kvasir om du anser att det är överkurs på universitetet. Jag minns att jag läste en bok på högstadiet där de förklarade sånt där på ett väldigt enkelt sätt så att även barn skulle kunna förstå det. Exempelvis stod det om ringar, ditt exempel 2+2=1 gäller i ringen Z3.

OK, men jag antar att det mest var kuriosum då för att öka nyfikenheten på riktig matematik. Får man fråga när du gick på högstadiet? Jag har en känsla av att pedagogiken har gått framåt och att man har försökt ge ett bredare grepp på matematiken t.o.m i låg- och mellanstadieblöckerna nu.

Jag hör iofs till den första generationen som skulle lära sig mängdlära redan i åk 1, men det var ju mest ett fiasko. Dels hade man inte någon större nytta av det på den nivån, och dels var det ju dessutom helt fel. Det var multimängder man lärde ut, inte mängder.

Kvasir skrev:OK, men jag antar att det mest var kuriosum då för att öka nyfikenheten på riktig matematik. Får man fråga när du gick på högstadiet? Jag har en känsla av att pedagogiken har gått framåt och att man har försökt ge ett bredare grepp på matematiken t.o.m i låg- och mellanstadieblöckerna nu.

Jag hör iofs till den första generationen som skulle lära sig mängdlära redan i åk 1, men det var ju mest ett fiasko. Dels hade man inte någon större nytta av det på den nivån, och dels var det ju dessutom helt fel. Det var multimängder man lärde ut, inte mängder.

Tittade i mattebok min faster hade i skolan på 60-talet och där stod det en massa om mängdlära. Förstår att det blev ett fiasko, vad har barn för nytta av att kunna det?

Själv gick jag i högstadiet i början på 90-talet, när man räknat ut den vanliga matteboken hade läraren böcker med lite mer avancerad matte som man fick läsa i.

Jag har gått alla gymnasiekurser i matematik (eller i alla fall A-E, finns eventeullt en F?) samt en högskolekurs i analytisk geometri.
Enligt betygen och prov så borde jag ha fattat allt, även om jag säkert har glömt en hel del saker nu).

Jag har ändå inte ens hört om mängdlära annat än som något en del klagar på var fel att ha i grundskolan eller som "något dumt".

Ringar och 2+2=1 har jag inte heller hört talas om.

Däremot vet jag säkert att 1+1=3 inom viss biologi
1+1=1 om det är 1(genuppsättning)+1(genuppsättning)=1(duploid individ)

Grundskolan gick jag på 70/80-talet (är född 1971). Gymnasiematematiken läste jag in 99/00 och universitetskursen läste jag 2005 eller något sådant.

Jag började skolan 1967 och blev pådyvlad mängdläran i femman (tror jag), jag förstod hur det funkade, men det var det enda i matten som jag inte förstod vad det skulle användas till...

Det har visat sig på senare år att mängdlära ([WikiSve]mängdteori[/WikiSve]) är bra för databaser och inget som ska läras ut till andra... Enligt Wikipedia var det en pedagogisk metod inom Den nya matematiken, men vad ska man med sådan pedagogik till är för mig fullständigt obegripligt.

Mängdlära är överhuvudtaget ett fundamentalt koncept i matematiken, men inget man behöver stifta närmare bekantskap med före gymnasiet. Det är praktiskt att kunna tala om mängder av naturliga, rationella och reella tal och delmängdsförhållandet däremellan redan på högstadiet, men det kräver inte någon större förståelse för mängdbegreppet. På gymnasiet däremot blir det mera användbart, när man börjar med sannolikhetslära. på högre nivåer blir det alltmer användbart, speciellt inom matematik som används inom t.ex. datalogi.


Jag började skolan 1969 och var, såvitt jag vet, den första årskursen som läste mängdlära redan i ettan. Jag kommer ihåg att vi hade sådana där flanelltavlor som man kunde fästa bilder av olika saker på och att det fanns bandliknande saker att fästa kring dessa för att markera mängder. Jag minns också att vi ibland fick gå upp på ett rum på vinden och titta på TV-program, svartvita förstås, med människor utklädda till olika djur som pratade om mängder. Inget av detta lämnade några starkade minnen, och jag tvivlar på att det bidrog nämnvärt till min förståelse av matematik.

Miche skrev:Jag började skolan 1967 och blev pådyvlad mängdläran i femman (tror jag), jag förstod hur det funkade, men det var det enda i matten som jag inte förstod vad det skulle användas till...

Det har visat sig på senare år att mängdlära ([WikiSve]mängdteori[/WikiSve]) är bra för databaser och inget som ska läras ut till andra... Enligt Wikipedia var det en pedagogisk metod inom Den nya matematiken, men vad ska man med sådan pedagogik till är för mig fullständigt obegripligt.

Kollade på din länk, men fattar mycket dåligt.
Mitt ordförråd är inget att skryta med. Jag faller på att jag fastnar på alla ord som jag inte vet exakt betydelse av, och även om jag vet exakt betydelse, så ska det oftast vridas till efter situation

Vissa ord kan jag aldrig lära mig, empiri, exakt betydelse av algebra (enligt förklaringar så betyder algebra bara att räkna? Och man fortsätter att räkna trots att man byter från algebra till geometri, så jag fattar inte. Allt går för mig ut på att lösa ett problem och få ett svar på en frågeställning genom att använda matematik.)
Alltså, jag har bara räknat på och det har fungerat utan att jag vet alla ord.
Tangent och sådant är ord som är mycket lättare att lära in då de betyder något som är enkelt att definiera.

Den här meningen:

I mängdteorin beskriver man vissa grundläggande egenskaper hos mängder med axiom för att se vad man kan bevisa i de olika teorierna.

från sidan du länkade till, säger mig ingenting. Vad är axiom? Vad är mängder med axiom? Är det massvis av axiom, eller speciella mängder som innehåller axiom (som typ celler med fler eller färre mitkondrier)? "Vad man kan bevisa i de olika teorierna"? Finns ju massor av teorier i världen. Ja, så där håller jag på texten igenom. Fy vad frustrerande.

Verbal aspergare med dålig verbal förmåga USCH.

Kvasir skrev:Mängdlära är överhuvudtaget ett fundamentalt koncept i matematiken, men inget man behöver stifta närmare bekantskap med före gymnasiet. Det är praktiskt att kunna tala om mängder av naturliga, rationella och reella tal och delmängdsförhållandet däremellan redan på högstadiet, men det kräver inte någon större förståelse för mängdbegreppet. På gymnasiet däremot blir det mera användbart, när man börjar med sannolikhetslära. på högre nivåer blir det alltmer användbart, speciellt inom matematik som används inom t.ex. datalogi.

Sannolikhetslära läste jag i en (eller kanske det återkommer i flera, på olika nivåer) gymnasiekurs.
Men jag har inte hört något om mängdlära.
Kan du beskriva närmare exakt vad en "mängd" av naturliga, reella, rationella tal m.m. innebär? Inte "naturliga tal" i sig, utan vad en MÄNGD av dem innebär.

Och exakt vad innebär det fetstilta: "Det är praktiskt att kunna tala om mängder av naturliga, rationella och reella tal och delmängdsförhållandet däremellan".

Gör jag rätt om jag antar att mängdlära har mindre betydelse i analytisk geometri som jag läste på universitet?

Bror Duktig skrev:Kollade på din länk, men fattar mycket dåligt.

Vilket ger en väldigt bra bild av mängdläran och dess betydelse för matematikutbildningen i skolan, dvs mängdläran är en helt värdelös pedagogik som man inte har någon som helst nytta av i grundskolan!

Du har med andra ord inte missat något!

Jag fick också läsa mängdlära någon gång på mellanstadiumet, lyckades lära mig hur det funkar, men jag fattade inte heller vad jag skulle använda det till sedan. Men det är klart, "alla skulle ju plugga det"...

Nä... alla de där kunskaperna i matte har jag egentligen aldrig haft någon vidare användning av... för mig räcker de fyra räknesätten alldeles tillräckligt. Och kanske procenträkning också, någon gång vart sjunde år eller så .

Bror Duktig skrev:Jag har ändå inte ens hört om mängdlära annat än som något en del klagar på var fel att ha i grundskolan eller som "något dumt".

Ringar och 2+2=1 har jag inte heller hört talas om.

Mängdlära är läran om samlingar av objekt. Exempelvis ingår alla huskatter och knähundar i gruppen tamdjur. Alla rävar och knähundar ingår i gruppen hunddjur. Trots detta ingår inga huskatter i gruppen hunddjur, och ytterst få rävar ingår i gruppen tamdjur.

Alla naturliga tal är heltal, däremot är inte alla heltal naturliga. I lågstadiematematiken är endast addition, multiplikation och subtrakton av mindre tal från större tillåtna. En sådan stympning av matematiken är en ring. I denna ring finns bara naturliga tal och man kommer inte på att råka på några andra. Skulle man tillåta att subtraktion användes fritt skulle man få en [WikiSve]kroppsutvidgning[/WikiSve] där även de negativa heltalen ingår. Inför man räknesätten division och kvadratrot får man en ring där alla komplexa tal ingår. Ju fler räknesätt man inför desto mer utvidgar man ringen att innefatta fler och fler tal.

En urtavla innehåller tal mellan 0 och 12. Om man tillåter de fyra räknesätten och endast tal mellan 0 och 12 får man en ring. I denna ring gäller det att:
1 + 1 =1
10 + 1 = 11
11 + 1 = 12 = 0
3 * 3 = 9
3 * 4 = 12 = 0
4 * 4 = 4 (16- 12, visaren fortsätter på nästa varv)
5 * 5 = 1 (25- 12 - 12, visaren går två varv)

Skulle man endast tillåta tal mellan 0 och 3 får man en annan ring. Här gäller det att:
1 + 1 = 2
1 + 2 = 3 = 0
2 + 2 = 1 (se det som att en visare går ett varv och stannar på 1)

tveskägg skrev:

Bror Duktig skrev:Jag har ändå inte ens hört om mängdlära annat än som något en del klagar på var fel att ha i grundskolan eller som "något dumt".

Ringar och 2+2=1 har jag inte heller hört talas om.

Mängdlära är läran om samlingar av objekt. Exempelvis ingår alla huskatter och knähundar i gruppen tamdjur. Alla rävar och knähundar ingår i gruppen hunddjur. Trots detta ingår inga huskatter i gruppen hunddjur, och ytterst få rävar ingår i gruppen tamdjur.

Alla naturliga tal är heltal, däremot är inte alla heltal naturliga. I lågstadiematematiken är endast addition, multiplikation och subtrakton av mindre tal från större tillåtna. En sådan stympning av matematiken är en ring. I denna ring finns bara naturliga tal och man kommer inte på att råka på några andra. Skulle man tillåta att subtraktion användes fritt skulle man få en [WikiSve]kroppsutvidgning[/WikiSve] där även de negativa heltalen ingår. Inför man räknesätten division och kvadratrot får man en ring där alla komplexa tal ingår. Ju fler räknesätt man inför desto mer utvidgar man ringen att innefatta fler och fler tal.

En urtavla innehåller tal mellan 0 och 12. Om man tillåter de fyra räknesätten och endast tal mellan 0 och 12 får man en ring. I denna ring gäller det att:
1 + 1 =1
10 + 1 = 11
11 + 1 = 12 = 0
3 * 3 = 9
3 * 4 = 12 = 0
4 * 4 = 4 (16- 12, visaren fortsätter på nästa varv)
5 * 5 = 1 (25- 12 - 12, visaren går två varv)

Skulle man endast tillåta tal mellan 0 och 3 får man en annan ring. Här gäller det att:
1 + 1 = 2
1 + 2 = 3 = 0
2 + 2 = 1 (se det som att en visare går ett varv och stannar på 1)

Tack, det sade ju mycket mer än allt jag läst eller hört innan.
Låter inte så konstigt i alla fall.
Och låter som det kan ha sysslats med under mina utbildningar (flera olika mängder) utan att jag hört något om mängder.

En sak fattar jag dock inte, varför är 1+1=1 på urtavlan?

Jag måste säga att orden/fackspråket verkar mer än lovligt krångligt för en som mig. För mig är "ringar" och "mängder" ord som jag använder på helt annat sätt.

Bror Duktig skrev:En sak fattar jag dock inte, varför är 1+1=1 på urtavlan?

Skrivfel, 2 blev 1.

Bror Duktig skrev:Jag måste säga att orden/fackspråket verkar mer än lovligt krångligt för en som mig. För mig är "ringar" och "mängder" ord som jag använder på helt annat sätt.

Ja, det är ett väldigt vanligt fenomen i akademiska texter som utestänger alla som inte har den rätta vokabulären. Det förtjänas att diskuteras i en ny tråd.

tveskägg skrev:

Bror Duktig skrev:En sak fattar jag dock inte, varför är 1+1=1 på urtavlan?

Skrivfel, 2 blev 1.

Bror Duktig skrev:Jag måste säga att orden/fackspråket verkar mer än lovligt krångligt för en som mig. För mig är "ringar" och "mängder" ord som jag använder på helt annat sätt.

Ja, det är ett väldigt vanligt fenomen i akademiska texter som utestänger alla som inte har den rätta vokabulären. Det förtjänas att diskuteras i en ny tråd.

Är det vanligt att folk har problem med orden, men ändå inte är dåliga inom själva ämnet?
Jag upplever mig som ha mycket mer problem med detta än gemene man.
Speciellt aspergare verkar ju vara ännu bättre på ord.

Jag har problem med att ord används olika och att förstå när det är fackord, vardagligt ord, även i situationer där folk tycker att det är jättelätt att förstå.

Jag tycker att det verkar vara mest de som är mer autistiska och har problem med språket, som har de problemen jag har (som jag har beskrivit i de senaste trådarna). Fast jag är ju rätt pratsam.

När jag väl har lärt mig ett ord, så använder jaq det gärna, helst i exakt betydelse. Vilket kan göra att jag låter mer verbalt duktig än jag är. Jag kan använda uttryck som "genetiska predispositioner" inslängda i ett språk som för övrigt låter som ett barns.

EDIT: hos tandläkaren kan jag säga antingen "andra premolaren" eller "den där lilla tanden där, som är lite större än de, men mindre än de, och som sitter här *pekar*. Alltså antingen exakt om jag kan orden, eller som ett barn. Så störande och jag känner mig ofast väldigt okunnig p.g.a. detta.

EDIT2: Jaaa, kan inte någon moderator bryta ut orddiskussionen till egen tråd och ge en bra rubrik? Jag diskuterar det gärna, då jag upplever mitt konstiga språkproblem som ett ganska stort hinder i mitt liv.

Bror duktig: Jag kan i princip aldrig komma ihåg namn, termer osv, även om logiken är solklar. Tex jag kan beskriva alla karaktärsdrag hos en djurart och vet exakt vilka den är släkt med, men vet inte vad släktena eller arten heter (på svenska).

carl skrev:Bror duktig: Jag kan i princip aldrig komma ihåg namn, termer osv, även om logiken är solklar. Tex jag kan beskriva alla karaktärsdrag hos en djurart och vet exakt vilka den är släkt med, men vet inte vad släktena eller arten heter (på svenska).

Frustrerande.
Jag har inte så jättebra minne heller, i alla fall inte det senaste decenniet då jag har varit sjuk. Så jag kan glömma fort.
Jag tror att det är arbetsminnet, eller inlagringen till långtidsminnet som det är fel på.
Speciellt inlärning av många nya saker samtidigt går dåligt.

Ibland kan jag inte heller beskriva eller komma ihåg saker förrän jag ser dem.
T.ex. ta isär en PVs bromsar och byta bromsbackar, jag kan göra det, men inte beskriva ur minnet eller komma ihåg delmomenten.
Fast det kanske beror på att det sysslan är rent praktisk, för som det här mer hårsaker har jag lättare att komma ihåg och beskriva, men då sker mesta inlärningen just via text och inte praktik.

Nu kanske jag i stället beskrev en andra problematik och inte det jag beskrev för några inlägg sedan.

Bror Duktig skrev:Kan du beskriva närmare exakt vad en "mängd" av naturliga, reella, rationella tal m.m. innebär? Inte "naturliga tal" i sig, utan vad en MÄNGD av dem innebär.

Du kan se det som en pluralform. En bil, flera bilar, alla bilar i hela världen tillsammans. En människa, flera människor, alla människor i hela världen tillsammans. Ett naturligt tal, flera naturliga tal, mängden naturliga tal.

Bror Duktig skrev:Och exakt vad innebär det fetstilta: "Det är praktiskt att kunna tala om mängder av naturliga, rationella och reella tal och delmängdsförhållandet däremellan".

Rationella tal (B) är tal som kan skrivas som en kvot av naturliga tal. Eftersom alla naturliga tal (A) kan skrivas som en kvot av andra naturliga tal så är alla naturliga tal rationella. Mängden naturliga tal är en delmängd av mängden rationella tal. Däremot är inte alla rationella tal naturliga (tex 1/3).



Låt A beteckna alla tal som börjar på 3, och B alla tal med oändlig decimalutveckling. Det finns en mängd som ingår både i A och B. I den mängden finns exempelvis talet pi.


Låt alla jämna tal få beteckningen A och alla udda beteckningen B. De naturliga talen är A och B tillsammans:


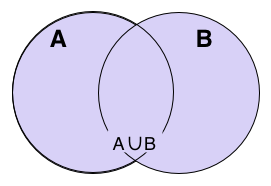
Ovanstående bilder är exempel på olika delmängdsförhållanden.

Tack tveskägg. Jag måste än en gång påpeka att man har valt konstiga ord i det här ämnet.

Jag har inte alls relaterat beteckningarna till det de står för i det här ämnet. Och det är typiskt sådant jag skulle ha mycket svårt att lära mig, och får lära in som "det heter det man inte tror att det heter" och liknande bakvändheter.

Ingen som har berättat vad semantik är?
Om jag inte minns fel är det ett begepp inom teoretisk filosofi eller språkfilosofi och innebär ungefär "vad vi lägger i ett begrepp".
Exempel:
Om du säger "hund", inbegriper begreppet "hund" såväl schäfer och labrador som kinesisk nakenhund och chow-chow, men det inbegriper INTE katter.
Hoppas det blev begripligt.

Semantik betyder tolkning, och används huvudsakligen inom logik, matematik och datalogi (och ofta även inom lingvistik och mera teoretiska språkstudier). Där använder man även begreppet syntax som betyder grammatik.

Dvs. syntaxen talar om hur man får skriva (matematiska formler, logiska formler, datorprogram etc.) och semantiken talar om vad det man har skrivit faktiskt betyder, dvs. hur det ska tolkas.

Inom "vanlig" matematik säger t.ex. syntaxreglerna att man får skriva "1 + 2" men inte "1 + + 2" eller "1 2 +". Semantiken säger att symbolen "1" ska tolkas som just talet ett och "2" som just talet två (vilket låter lite oprecist, men skulle kräva mera avancerad matematik att precisera), samt att symbolen "+" tolkas som "vanlig" addition av de två talen på ömse sidor. Vi är så vana vid att göra just den tolkningen att det kan verka självklart och konstigt att ens antyda att det skulle kunna vara annorlunda, men det kan det mycket väl vara, även om vi i praktiken sällan har anledning att definiera det annorlunda. Inom logiken är det ett fundamentalt koncept att skilja just på syntax och semantik och att inte lägga någon förutfattad tolkning i symbolerna. Likaså inom datalogi och programmering.

Den som nu inte förstår skillnaden mellan syntax och semantik ska inte förtvivla. Dels är ovanstående förklaring knappast den bästa jag har presterat i ämnet, och dels vet jag av erfarenhet från undervisning att just detta är något av det svåraste i hela utbildningen för många universitetstudenter att förstå. Jag skulle vilja gå så långt som att påstå att problemet med att skilja på syntax och semantik egentligen är ett problem som är mycket vanligt på diverse olika områden, även somliga som är väsensskilda från de jag nämnde ovan, och svårigheterna att förstå denna skillnad går igen. T.ex. menar jag att vi har ungefär samma problem inom konsten, att skilja på bilden som bild (syntax) och bildens innehåll (semantiken, vad den föreställer, om den föreställer något). konststudenter verkar ofta har ungefär lika svårt att förstå den skillnaden som logikstudenter att förstå skillnaden på syntax och semantik i logiken.