Talserier och lek med tal
9 inlägg
• Sida 1 av 1
Talserier och lek med tal
Är det nån mer som gillar att leka med tal och hitta samband?
Den mest kända är ju 9:ans gångertabell.
1x9=9
2x9=18, 1+8=9
3x9=27, 2+7=9
o.s.v. i all oändlighet.
5:ans gångertabell är också lite kul.
1x5=5
3x5=15, 1+5=6
5x5=25, 2+5=7
7x5=35, 3+5=8
9x5=45, 4+5=9
11x5=55, 5+5=10
13x5=65, 6+5=11
15x5=75, 7+5=12
17x5=85, 8+5=13
19x5=95, 9+5=14
21x5=105, 10+5=15
o.s.v. i all onändlighet
tar man ett udda tal gånger fem, och sen adderar sifforna, får man ett resultat som alltid är 1 siffra större än föregående udda tal gånger 5.
2x5=10
4x5=20
6x5=30
8x5=40
10x5=50
12x5=60
14x5=70
16x5=80
18x5=90
20x5=100
22x5=120
o.s.v. i all oändlighet
ta bort nollan så ökar det med 1 varje gång man multiplicerar ett jämnt tal med 5
4:ans gångertabell:
1x4=4
3x4=12, 1+2=3
5x4=20, 2+0=2
7x4=28, 2+8=10, 1+0=1
9x4=36, 3+6=9
11x4=44, 4+4=8
13x4=52, 5+2=7
o.s.v.
här minskar det med 1 varje gång man tar 4 gånger ett udda tal
4x2=8
4x4=16, 1+6=7
4x6=24, 2+4=6
4x8=32, 3+2=5
o.s.v
om man multiplicerar 4 med et jämt tal minskas det med 1 även här.
Fyll bara på med fler grejor i samma stil. All lek med siffror och tal är godkända i denna tråd. Men svåra mattetal hör inte hemma här, det ska vara enkelt att se sambandet.
Den mest kända är ju 9:ans gångertabell.
1x9=9
2x9=18, 1+8=9
3x9=27, 2+7=9
o.s.v. i all oändlighet.
5:ans gångertabell är också lite kul.
1x5=5
3x5=15, 1+5=6
5x5=25, 2+5=7
7x5=35, 3+5=8
9x5=45, 4+5=9
11x5=55, 5+5=10
13x5=65, 6+5=11
15x5=75, 7+5=12
17x5=85, 8+5=13
19x5=95, 9+5=14
21x5=105, 10+5=15
o.s.v. i all onändlighet
tar man ett udda tal gånger fem, och sen adderar sifforna, får man ett resultat som alltid är 1 siffra större än föregående udda tal gånger 5.
2x5=10
4x5=20
6x5=30
8x5=40
10x5=50
12x5=60
14x5=70
16x5=80
18x5=90
20x5=100
22x5=120
o.s.v. i all oändlighet
ta bort nollan så ökar det med 1 varje gång man multiplicerar ett jämnt tal med 5
4:ans gångertabell:
1x4=4
3x4=12, 1+2=3
5x4=20, 2+0=2
7x4=28, 2+8=10, 1+0=1
9x4=36, 3+6=9
11x4=44, 4+4=8
13x4=52, 5+2=7
o.s.v.
här minskar det med 1 varje gång man tar 4 gånger ett udda tal
4x2=8
4x4=16, 1+6=7
4x6=24, 2+4=6
4x8=32, 3+2=5
o.s.v
om man multiplicerar 4 med et jämt tal minskas det med 1 även här.
Fyll bara på med fler grejor i samma stil. All lek med siffror och tal är godkända i denna tråd. Men svåra mattetal hör inte hemma här, det ska vara enkelt att se sambandet.
- Lilla Gumman
- Inlägg: 5451
- Anslöt: 2007-08-01
- Ort: Ludvika
Re: Talserier och lek med tal
Trodde det fanns nån här som gillade sånt här?
- Lilla Gumman
- Inlägg: 5451
- Anslöt: 2007-08-01
- Ort: Ludvika
Re: Talserier och lek med tal
7:ans tabell. Lite mindre uppenbart, men ...
7x1=7
7x2=14, 7-3=4 (6, 5, 4)
7x3=21, 4-3=1 (3, 2, 1)
7x4=28, 1-3=8 (0,9,
o.s.v.
Ta bort första siffran i svaret, den sista siffran minskar hela tiden med 3. Alltså en rundgång, man räknar 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 o.s.v.
7x1=7
7x2=14, 7-3=4 (6, 5, 4)
7x3=21, 4-3=1 (3, 2, 1)
7x4=28, 1-3=8 (0,9,
o.s.v.
Ta bort första siffran i svaret, den sista siffran minskar hela tiden med 3. Alltså en rundgång, man räknar 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 o.s.v.
- Lilla Gumman
- Inlägg: 5451
- Anslöt: 2007-08-01
- Ort: Ludvika
Talserier och lek med tal
Om man skriver alla tvåsiffriga tal i en 10x10-kvadrat framträder en del roliga mönster.
I den ena diagonalen (gulmarkerad) finns alla tal som innehåller två likadana siffror och den andra (blåmarkerad) innehåller nians multiplikationstabell. Talen nedanför/till vänster om den gula diagonalen har samma siffror som motsvarande tal ovanför/till höger fast i omvänd ordning. För varje tal på vardera sidan om den blåa diagonalen gäller att den första siffran plus den andra siffran i motsvarande tal på andra sidan alltid är lika med nio.

Om vi lägger ihop siffrorna i varje tal i figuren ovan (0 + 0; 0 + 1; 0 + 2 … 9 + 7; 9 + 8; 9 + 9) så får vi en kvadrat där en diagonal (grönmarkerad) består av de jämna talen mellan noll och arton, medan den andra diagonalen (rödmarkerad) består av nior. Ovanför/till vänster om den sistnämnda finns talen noll till åtta och på motsatta sidan talen tio till arton. Summan av ett tal på ena sidan och motsvarande tal på andra sidan av den röda diagonalen blir alltid lika med arton.

I den ena diagonalen (gulmarkerad) finns alla tal som innehåller två likadana siffror och den andra (blåmarkerad) innehåller nians multiplikationstabell. Talen nedanför/till vänster om den gula diagonalen har samma siffror som motsvarande tal ovanför/till höger fast i omvänd ordning. För varje tal på vardera sidan om den blåa diagonalen gäller att den första siffran plus den andra siffran i motsvarande tal på andra sidan alltid är lika med nio.

Om vi lägger ihop siffrorna i varje tal i figuren ovan (0 + 0; 0 + 1; 0 + 2 … 9 + 7; 9 + 8; 9 + 9) så får vi en kvadrat där en diagonal (grönmarkerad) består av de jämna talen mellan noll och arton, medan den andra diagonalen (rödmarkerad) består av nior. Ovanför/till vänster om den sistnämnda finns talen noll till åtta och på motsatta sidan talen tio till arton. Summan av ett tal på ena sidan och motsvarande tal på andra sidan av den röda diagonalen blir alltid lika med arton.

Talserier och lek med tal
Sjundedelar:
1/7 = 0,142857142857...
2/7 = 0,285714285714...
3/7 = 0,428571428571...
4/7 = 0,571428571428...
5/7 = 0,714285714285...
6/7 = 0,857142857142...
Samma sifferserie 1, 4, 2, 8, 5, 7 upprepas i all oändlighet.
1/7 = 0,142857142857...
2/7 = 0,285714285714...
3/7 = 0,428571428571...
4/7 = 0,571428571428...
5/7 = 0,714285714285...
6/7 = 0,857142857142...
Samma sifferserie 1, 4, 2, 8, 5, 7 upprepas i all oändlighet.
Talserier och lek med tal
Geastrum skrev:Sjundedelar:
1/7 = 0,142857142857...
2/7 = 0,285714285714...
3/7 = 0,428571428571...
4/7 = 0,571428571428...
5/7 = 0,714285714285...
6/7 = 0,857142857142...
Samma sifferserie 1, 4, 2, 8, 5, 7 upprepas i all oändlighet.
Hej Geastrum!
Jag kontrar med sjuttondelar:
1/17 = 0.05882352941176470588235294117647058823529411764705882352941176470588235294117647058823529411764705882352941176470588235294117647058823529411764705882352941176470588235294117647058823529411764705882352941176470588235294117647058...
2/17 = 0.11764705882352941176470588235294117647058823529411764705882352941176470588235294117647058823529411764705882352941176470588235294117647058823529411764705882352941176470588235294117647058823529411764705882352941176470588235294117...
3/17 = 0.17647058823529411764705882352941176470588235294117647058823529411764705882352941176470588235294117647058823529411...
osv.
Notera att även de inledande siffrorna egentligen ingår i en trunkerad cyklisk permutation av talserien som upprepar sig.
Fler sådana tal med sådan egenskap kan du hitta här: Full reptend primes: primes with primitive root 10
Talserier och lek med tal
Nians multiplikationstabell med elftedelar:

Notera hur talen "speglas" runt demarkationslinjen 45-54, 36<->63 27<-->72 18<--->81 osv för 09 90, visst är det vackert?
Vi ser också att vi kan lägga ihop multipler av 9 genom 100-potenser för att bilda elftedelar:

Lite oväntat har vi alltså hittat ett begränsat värde för en oändlig summa:
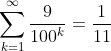
Notera hur talen "speglas" runt demarkationslinjen 45-54, 36<->63 27<-->72 18<--->81 osv för 09 90, visst är det vackert?

Vi ser också att vi kan lägga ihop multipler av 9 genom 100-potenser för att bilda elftedelar:
Lite oväntat har vi alltså hittat ett begränsat värde för en oändlig summa:
Talserier och lek med tal
Ta ett valfritt fyrasiffrigt heltal, t.ex. 2017 ...
Arrangera siffrorna i storleksordning, med den största siffran först:
7210
Ta nu detta tal minus det tal man får om man vänder på siffrorna:
7210 - 0127 = 7083
Arrangera om siffrorna i det resulterande talet och upprepa på samma sätt:
8730 - 0378 = 8352
8532 - 2358 = 6174
7641 - 1467 = 6174 (!)
När man får resultatet 6174 så kommer man inte längre. Det märkliga är att alla fyrasiffriga heltal (utom... se nedan) ger exakt samma resultat efter max sju steg. Det är nästan magiskt. Talet 6174 kallas Kaprekars konstant efter den indiske matematikern Dattathreya Ramchandra Kaprekar.
De enda tal som inte funkar är 1111, 2222, 3333, 4444, 5555, 6666, 7777, 8888 och 9999 eftersom de ger resultatet noll vid den första subtraktionen. Det går också bra att använda tal som är mindre än 1000 så länge man fyller på med en, två eller tre nollor före den första siffran så att man får totalt fyra siffror.
https://www.math.hmc.edu/funfacts/ffile ... .5-8.shtml
Arrangera siffrorna i storleksordning, med den största siffran först:
7210
Ta nu detta tal minus det tal man får om man vänder på siffrorna:
7210 - 0127 = 7083
Arrangera om siffrorna i det resulterande talet och upprepa på samma sätt:
8730 - 0378 = 8352
8532 - 2358 = 6174
7641 - 1467 = 6174 (!)
När man får resultatet 6174 så kommer man inte längre. Det märkliga är att alla fyrasiffriga heltal (utom... se nedan) ger exakt samma resultat efter max sju steg. Det är nästan magiskt. Talet 6174 kallas Kaprekars konstant efter den indiske matematikern Dattathreya Ramchandra Kaprekar.
De enda tal som inte funkar är 1111, 2222, 3333, 4444, 5555, 6666, 7777, 8888 och 9999 eftersom de ger resultatet noll vid den första subtraktionen. Det går också bra att använda tal som är mindre än 1000 så länge man fyller på med en, två eller tre nollor före den första siffran så att man får totalt fyra siffror.
https://www.math.hmc.edu/funfacts/ffile ... .5-8.shtml
Talserier och lek med tal
Ibland kan jag leka med siffror och bokstavskombinationer. Max Tegmark har ju lanserat teorin att verkligheten är matematiska ekvationer. Varför dyker gyllene snittet upp överallt? Är inne på den här sidan ibland. https://plus.maths.org/content/
- Dreamtrance
- Inlägg: 1045
- Anslöt: 2016-07-04
Återgå till Intressanta intressen