Ordförståelse (och lite matematik).
40 inlägg
• Sida 2 av 2 • 1, 2
Bror Duktig skrev:Vissa ord kan jag aldrig lära mig, empiri, exakt betydelse av algebra (enligt förklaringar så betyder algebra bara att räkna? Och man fortsätter att räkna trots att man byter från algebra till geometri, så jag fattar inte. Allt går för mig ut på att lösa ett problem och få ett svar på en frågeställning genom att använda matematik.)
Algebra = att lösa matematiska problem genom att använda de fyra räknesätten, upphöjt till och roten ur ett ändligt antal gånger.
Ett geometriskt problem är att ta reda på proportionerna av sidorna i en triangel där vinklarna är kända:
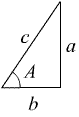
Sinus kan användas för att ta reda på proportionerna mellan a och c. Den är uppbyggd av de fyra räknesätten och potens på följande sätt:
sin(A) = Aˆ1/1-Aˆ3/(1*2*3)+Aˆ5/(1*2*3*4*5)-Aˆ7/(1*2*3*4*5*6*7)+...
För att få ett exakt värde på proportionerna i triangeln måste man alltså utföra ett oändligt antal additioner, subtraktioner, divisioner, multiplikationer och upphöjningar. Då är det inte algebra längre.
Senast redigerad av tveskägg 2011-05-04 22:13:11, redigerad totalt 1 gång.
Bror Duktig skrev:Den här meningen:från sidan du länkade till, säger mig ingenting. Vad är axiom? Vad är mängder med axiom? Är det massvis av axiom, eller speciella mängder som innehåller axiom (som typ celler med fler eller färre mitkondrier)? "Vad man kan bevisa i de olika teorierna"? Finns ju massor av teorier i världen. Ja, så där håller jag på texten igenom. Fy vad frustrerande.I mängdteorin beskriver man vissa grundläggande egenskaper hos mängder med axiom för att se vad man kan bevisa i de olika teorierna.
Axiom betyder regler för hur beräkningar skall gå till. Exempelvis hur oändligt stora mängder skall hanteras. Beroende på hur man varierar reglerna för detta så kan man få fram olika resultat.
Senast redigerad av tveskägg 2011-05-04 22:13:11, redigerad totalt 1 gång.
Kvasir skrev:Dvs. syntaxen talar om hur man får skriva (matematiska formler, logiska formler, datorprogram etc.) och semantiken talar om vad det man har skrivit faktiskt betyder, dvs. hur det ska tolkas.
Inom "vanlig" matematik säger t.ex. syntaxreglerna att man får skriva "1 + 2" men inte "1 + + 2" eller "1 2 +".
Uttrycket 1 2 + är omvänd polsk notation vilken tillämpas bl.a. av min miniräknare. Det blir färre knapptryckningar. Ta ex.vis uttrycket
a x (b + c) / (d + e) som kräver 14 tryck med en vanlig räknare för att få svaret. Med omvänd polsk notation gör man samma sak med 11 tryck:
b [ENTER] c + d [ENTER] e + / a x
man kan också skoja till det genom att trycka
a [ENTER] b [ENTER] c [ENTER] + d [ENTER] e + / x
Det skojaste är dock när nån lånar räknaren och febrilt letar efter likhetstecknet som inte finns.
Fast jag vet egentligen inte om matematiska skämt är så skojiga
Senast redigerad av Duras 2011-05-04 22:13:11, redigerad totalt 1 gång.
Bror Duktig skrev:Kvasir skrev:Bror Duktig skrev:Det låter som mitt problem.
Jag argumenterar så dåligt att jag skulle förlora en diskussion om huruvida 1+1 är 2 eller 3 (om jag påstod att det vore 2 alltså).
Ja, vadå då? Det beror helt på vilken algebra du väljer och vilken semantik du använder för siffersymbolerna.
När blir 1+1=3?
I parrelationer kanske?
Jag vet inte vad semantik betyder.
Avrundning..? 1.4 avrundas vanligtvis till 1 med en värdesiffra.
Så.. 1 kan därmed lika gärna vara 1.4 dvs 1+1 kan vara 2.8 vilket avrundas till 3.
Senast redigerad av jorand 2011-05-04 22:13:11, redigerad totalt 1 gång.
Duras skrev:Uttrycket 1 2 + är omvänd polsk notation vilken tillämpas bl.a. av min miniräknare. Det blir färre knapptryckningar. Ta ex.vis uttrycket
I begreppet "vanlig" matematik avsåg jag naturligtvis infixnotation, men jag funderade på att kommentera det, eftersom jag misstänkte att denna kommentar skulle dyka upp. Den omvända polska notationen kallas vanligen för postfixnotation. Det finns också det motsatta, prefixnotation, som används t.ex. i vissa programspråk, som Lisp. Den stora fördelen med prefix- och infixnotationerna är att man inte behöver parenteser för styra/bryta prioritetsordningen, vilket man som bekant behöver i infixnotationen. Fast om det är någon fördel för människor är tveksamt.
Senast redigerad av Kvasir 2011-05-04 22:13:11, redigerad totalt 1 gång.
Kvasir skrev:Den stora fördelen med prefix- och infixnotationerna är att man inte behöver parenteser för styra/bryta prioritetsordningen, vilket man som bekant behöver i infixnotationen. Fast om det är någon fördel för människor är tveksamt.
HP-fanatiker hävdar att det är en fördel för människor (åtminstone för HP-fanatikerna...) och jag tycker att hela iden med RPN är väldigt smart för det tvingar en till att tänka lite extra så man inte bara knappar rakt av utan att se att det blir rätt och resultatet blir rimligt!
Senast redigerad av Miche 2011-05-04 22:13:11, redigerad totalt 1 gång.
1 + 1 = 3 i Graykod med litet god vilja:
Talet 1 skrivs i Graykod som 0...001, som om det tolkas som ett vanligt binärt tal blir 1.
Talet 2 skrivs i Graykod som 0...011, som om det tolkas som ett vanligt binärt tal blir 3.
Additionen 1 + 1 = 2 skrivs därför i Graykod som 0...001 + 0...001 = 0...011, som om det tolkas som vanliga binära tal blir 1 + 1 = 3.
Talet 1 skrivs i Graykod som 0...001, som om det tolkas som ett vanligt binärt tal blir 1.
Talet 2 skrivs i Graykod som 0...011, som om det tolkas som ett vanligt binärt tal blir 3.
Additionen 1 + 1 = 2 skrivs därför i Graykod som 0...001 + 0...001 = 0...011, som om det tolkas som vanliga binära tal blir 1 + 1 = 3.
Senast redigerad av md2perpe 2011-05-04 22:13:11, redigerad totalt 1 gång.
tveskägg skrev:Axiom betyder regler för hur beräkningar skall gå till.
Strängt taget nej.
Axiom är de grundläggande sanningar som man antar utan att bevisa dem för att man ska "komma igång", slutedningsreglerna behöver ju i allmänhet något att arbeta med.
Senast redigerad av nallen 2011-05-04 22:13:11, redigerad totalt 1 gång.
nallen skrev:tveskägg skrev:Axiom betyder regler för hur beräkningar skall gå till.
Strängt taget nej.
Axiom är de grundläggande sanningar som man antar utan att bevisa dem för att man ska "komma igång", slutedningsreglerna behöver ju i allmänhet något att arbeta med.
nallen har helt rätt. Förvånande att jag missade det trots att jag läst denna tråd.
Senast redigerad av weasley 2011-05-04 22:13:11, redigerad totalt 1 gång.
Axiom?
nallen skrev:.
Axiom är de grundläggande sanningar som man antar utan att bevisa dem för att man ska "komma igång", slutedningsreglerna behöver ju i allmänhet något att arbeta med.
Kurt Gödel har nog bevisat axiomens tvesamma giltighet,men tyvär fattade jag inte mycket av det
 .
.Man får nog vara mattesvant för att fatta.
Går att hitta en hel del om Gödel på Wikipedia
Senast redigerad av lasseivägen 2011-05-04 22:13:11, redigerad totalt 1 gång.
- lasseivägen
- Inlägg: 4798
- Anslöt: 2009-07-20
- Ort: På havet kaparkapten inte Rövare
Re: Axiom?
lasseivägen skrev:nallen skrev:.
Axiom är de grundläggande sanningar som man antar utan att bevisa dem för att man ska "komma igång", slutedningsreglerna behöver ju i allmänhet något att arbeta med.
Kurt Gödel har nog bevisat axiomens tvesamma giltighet,men tyvär fattade jag inte mycket av det.
Man får nog vara mattesvant för att fatta.
Går att hitta en hel del om Gödel på Wikipedia
Då har du nog missförstått Gödel. Axiom är per definition sanna (som utgångspunkt för den slutsatsdragning man vill göra).
Ordförståelse (och lite matematik).
Kvasir skrev:Semantik betyder tolkning, och används huvudsakligen inom logik, matematik och datalogi (och ofta även inom lingvistik och mera teoretiska språkstudier). Där använder man även begreppet syntax som betyder grammatik.
Dvs. syntaxen talar om hur man får skriva (matematiska formler, logiska formler, datorprogram etc.) och semantiken talar om vad det man har skrivit faktiskt betyder, dvs. hur det ska tolkas.
Inom "vanlig" matematik säger t.ex. syntaxreglerna att man får skriva "1 + 2" men inte "1 + + 2" eller "1 2 +". Semantiken säger att symbolen "1" ska tolkas som just talet ett och "2" som just talet två (vilket låter lite oprecist, men skulle kräva mera avancerad matematik att precisera), samt att symbolen "+" tolkas som "vanlig" addition av de två talen på ömse sidor. Vi är så vana vid att göra just den tolkningen att det kan verka självklart och konstigt att ens antyda att det skulle kunna vara annorlunda, men det kan det mycket väl vara, även om vi i praktiken sällan har anledning att definiera det annorlunda. Inom logiken är det ett fundamentalt koncept att skilja just på syntax och semantik och att inte lägga någon förutfattad tolkning i symbolerna. Likaså inom datalogi och programmering.
Den som nu inte förstår skillnaden mellan syntax och semantik ska inte förtvivla. Dels är ovanstående förklaring knappast den bästa jag har presterat i ämnet, och dels vet jag av erfarenhet från undervisning att just detta är något av det svåraste i hela utbildningen för många universitetstudenter att förstå. Jag skulle vilja gå så långt som att påstå att problemet med att skilja på syntax och semantik egentligen är ett problem som är mycket vanligt på diverse olika områden, även somliga som är väsensskilda från de jag nämnde ovan, och svårigheterna att förstå denna skillnad går igen. T.ex. menar jag att vi har ungefär samma problem inom konsten, att skilja på bilden som bild (syntax) och bildens innehåll (semantiken, vad den föreställer, om den föreställer något). konststudenter verkar ofta har ungefär lika svårt att förstå den skillnaden som logikstudenter att förstå skillnaden på syntax och semantik i logiken.
Ha, jag hittade i alla fall en tråd att lägga en så spännande grej (som datorn hade som dagens citat någon gång):
"All meanings, we know, depend on the key of interpretation."
George Eliot
Read more at http://www.brainyquote.com/quotes/quotes/g/georgeelio164014.html
/notwoodstock
- notwoodstock
- Inlägg: 3942
- Anslöt: 2013-12-22
- Ort: Stockholm
Ordförståelse (och lite matematik).
Jag blir galen när människor skriver "hälften så liten" - oavsett vad de menar, men vanligtvis verkar de mena "hälften så stor" - och när människor(även s k forskare) skriver "tusen gånger mindre". Ska det vara så svårt att skriva "en tusendedel så stor" eller "tusen gånger så stor"? Tre gånger större är lika med fyra gånger så stor! Enkelt att kontrollera: En gång större är två gånger så stor!
Ordförståelse (och lite matematik).
Nej, "dubbelt så liten" ska det vara.gadas skrev:Jag blir galen när människor skriver "hälften så liten" -
Ordförståelse (och lite matematik).
Gu'vet vad det ska vara - men det finns både "dubbelt så liten" och "hälften så liten"...
Ordförståelse (och lite matematik).
Nu orkar jag inte läsa denna tråd längre. Kanske återkommer, för jag är nyfiken på Grupper och Ringar.
Jag har annars lite koll på saker och föreslår helt enkelt som exempel på en Algebra, det när man håller på med binära tal. Eller Boolsk Algebra.
Om man har binära tal, så är ju 1 + 1 = 10 (fast då uttalas ju svaret "ett noll").
Och Inom Boolsk Algebra, så är + vanligtvis "OR"-operatorn. Och då är 1 + 1 = 1.
Och inom en högskoleutbildning så krävs det nog att man går Teknisk Fysik (eller var så på 70-talet i alla fall) för att läsa Abstract Algebra, som jag tror det kan heta.
Och jag tycker inte det är elakt att vidga vyerna för folk! (Ok, något "osjysst", kanske).
/notwoodstock
Jag har annars lite koll på saker och föreslår helt enkelt som exempel på en Algebra, det när man håller på med binära tal. Eller Boolsk Algebra.
Om man har binära tal, så är ju 1 + 1 = 10 (fast då uttalas ju svaret "ett noll").
Och Inom Boolsk Algebra, så är + vanligtvis "OR"-operatorn. Och då är 1 + 1 = 1.
Och inom en högskoleutbildning så krävs det nog att man går Teknisk Fysik (eller var så på 70-talet i alla fall) för att läsa Abstract Algebra, som jag tror det kan heta.
Och jag tycker inte det är elakt att vidga vyerna för folk! (Ok, något "osjysst", kanske).
/notwoodstock
- notwoodstock
- Inlägg: 3942
- Anslöt: 2013-12-22
- Ort: Stockholm
Återgå till Intressanta intressen